I got a good comment on my previous article about implementing the Game of Life in CUDA pointing out that I was leaving a lot of performance at the table by only considering a single step at once.

Their point was that my implementations were bound by the speed of DRAM. An A40 can send 696 GB/s from DRAM memory to the cores, and my setup required sending at least one bit in each direction per-cell per-step, which worked out at 1.4ms.

But DRAM is the slowest memory on a graphics card. The L1 cache is hosted inside each Streaming Multiprocessor, much closer to where the calculations can occur. It’s tiny, but has an incredible bandwidth – potentialy 67 TB/s. Fully utilizing this is nigh impossible, but even with mediocre utilization we’d do far better than before.

We can’t just store an entire array in L1 as it’s tiny and not persistent. But we can explicitly store stuff in L1 while a CUDA kernel is running with a shared memory array. So the trick is, we’ll reduce round trips to DRAM. Each threadblock will do the following:

• Load a rectangle from DRAM to shared memory
• Then perform 8 steps of Game of Life that operate purely on shared memory.
• Write back to DRAM a rectangle shrunk by 8 cells, as cells near the border won’t be computed correctly.

There are few inconveniences this way:

• The threads of the threadblock operate concurrently, so we cannot safely write to the same memory that is being read from. We actually need two shared memory arrays, and swap them over with double buffering.
• We need to call __syncthreads() after each step to ensure that all the threads see updates to shared memory from other threads.
• Due to the rectangle shrinkage, we’ll need to overlap threadblocks a bit, which leads to slightly worse utilization.

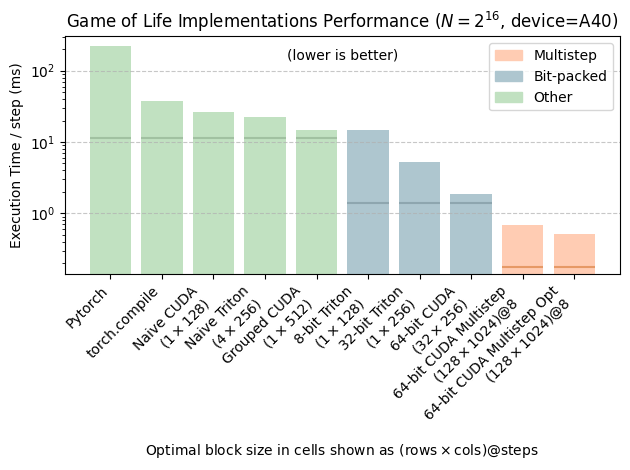
The full code, which integrates with the bitpacking and grouping we introduced in the previous article is pretty long, but you can find it here. It takes 5.4ms to run the kernel, which means we’re not near the DRAM bandwidth any more. But that’s for 8 steps, so the execution time per step is 0.68 ms, which is 270% faster than the best variant from the previous article.

It looks like we’re not DRAM bottlenecked anymore. Instead, we’ve put in so many instructions a single threadblock that the time is spent evaluating them. This is why increasing the step count further than 8 didn’t yield any benefits.

I was able to squeeze a bit more performance by optimising the computation. The trick is to unroll the ROW_GROUP loop, and then share some calculations between rows. Specifically, because Game of Life requires you to sum up a $3\times 3$ rectangle, you can pre-compute the $1\times 3$ rectangles, and then sum the 3 of those needed for each row.

This gives an final performance chart as follows. I had to switch to log scales as the difference is so dramatic.

I also tried a variant where, in addition to using a shared memory array, I used a register array in a small inner loop. Registers have even faster access speed than shared memory and can be treated like array provided the compiler is capable of unrolling all loops. Unfortunately, this didn’t yield any performance benefit. Possibly having such a massive amount of registers affected how much could run concurrently, reducing utilisation.