Intermediate

This category contains more advanced articles that build on background knowledge or previous articles.

See Beginner and Advanced for more articles.

Ortho-tiles

| Boris

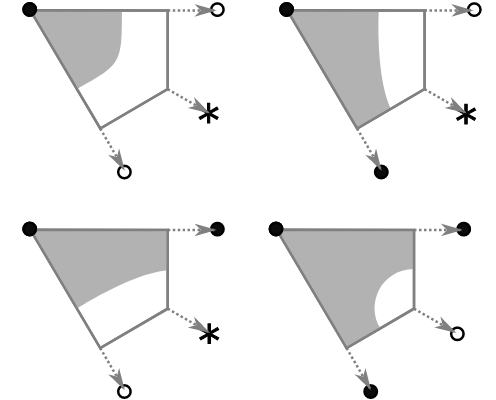
Last time, we looked at quarter-tiles. This was an auto-tiling technique for square grids. Each cell in the grid is associated with a terrain (i.e. either solid or empty). Then the squares were split in four, and each quarter was assigned an appropriate quarter-tile.

Otho-tiles extends this procedure to work with irregular grids, even non-square grids. We just have to alter the procedure a little, and be ready to deform the quarter tiles fit in place.

Ortho?

Ortho is a Conway Operator. It can be thought of as the extension of dividing a square into 4. It divides each n-gon into n “kites” or “ortho-cells”. Each kite is a four sided shape containing the cell center, one corner, and the midpoint of the two edges adjacent to that corner.

Kites for some shapes

The appeal of the ortho operation is it can take any polygonal grid, no matter how irregular, and convert it into a grid of 4 sided shapes. And it’s much easier to work with something that has a consistent number of sides.

Continue reading →

Quarter-Tile Autotiling

| Boris

Since Oskar posted about it, I see an increasing amount of praise for his Dual Grid proposal for autotiling terrains. It works by drawing tiles at a half-cell offset to the base grid, creating a dual grid, and using marching squares autotiling to select which tile to draw based on the terrains the corners of the dual grid, which is the centers of base grid.

This is a great scheme. It’s simple, only needs a few tiles and can be extended quite easily. It’s used in many games.

But, it does have some drawbacks. The dual grid is difficult to get your head around. You have to worry about ambiguous tiles. And despite being a substantial improvement over the blob pattern, it still requires drawing quite a number of different tiles.

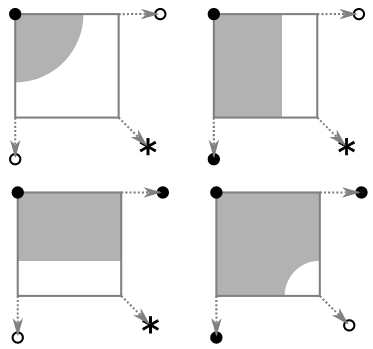
I’m here to explain an alternative, quarter-tile autotiling. Quarter-tiling has also been called sub-tiles, meta-tiles (when doubling instead of halving). I’ve previous described as micro blob, which is the same thing with precomposition. It’s best known for being the tiling built into the RPG Maker engine.

Quarter-tiling is pretty easy to implement, and requires substantially less effort to create tiles for, as it uses fewer, smaller tiles. That does mean it’s not possible to produce as much tile variation as marching squares. But there’s plenty of techniques for adding that back.

Later, we’ll look at ortho-tiles – an extension of quarter-tiles to irregular, non-square, grids.

Continue reading →

Constrained Text Generation with AI

| Boris

I was discussing how AI text generation, such as ChatGPT, might end up getting used in computer games. So far, designers are fairly reluctant to adopt the technology. One of the key problems is that you just can’t control the output enough. Language models will break character or respond in inappropriate and toxic ways. Finding a good solution to this is a huge research field, and not likely to get cracked soon.

For the foreseeable future, AI in games is much more likely to be used offline – assets and dialog generation generated up front, so it can be vetted before being integrated into the game.

But it got me thinking, can we vet the AI’s output in advance, but still get the benefits of intelligent decision making at runtime? It turns out, we can! I doubt it’ll be useful in every circumstance, but I can certainly see uses for it, like chatbots, games.

The code and demonstration for this article is available here.

Continue reading →

2d Marching Cubes with Multiple Colors

| Boris

2d Marching cubes (sometimes called marching squares) is a way of drawing a contour around an area. Alternatively, you can think of it as a drawing a dividing line between two different areas. The areas are determined by a boolean or signed number value on each vertex of a grid:

But what if we didn’t have a boolean value? What if we had n possible colors for each vertex, and we wanted to draw separating lines between all of them?

Continue reading →

Classification of Tilesets

| Boris

Many years ago I started looking at different sorts of tiles sets used by artists. A good tile set is flexible enough to allow tiles to be re-used in a lot of situation, but simple enough that the tiles can be easily created. Ideally, it would enable autotiling or otherwise be easy to design levels with.

Though I covered a few different techniques back then, I fell short of any systematic discussion of tiles. Here I plan to take a more rigorous approach, in the hopes of making a common language for referring to different tile sets, and pointing out the key variations in design. Maybe we’ll even discover something new, like Mendelev predicting new elements for the periodic table.

Continue reading →

Infinite Modifying in Blocks

| Boris

I’m going to share with you a technique I’ve found for doing lazy, reliable, deterministic, constant-time infinite generation of tile based levels using Wave Function Collapse (WFC). But first, let’s cover some background, Modifying in Blocks, and lazy chunk based infinite generation.

Continue reading →