Everyone loves the Townscaper grid. It’s got a a nice organic look, while still being quadrilateral tiles, somewhat regular, and reasonably easy to implement. But it has some annoyances. I’ve finally managed to find my own design of grid that has a very similar look, but fixes these problems.
What’s wrong with the Townscaper Grid?
You can see an animation of how the grid is greated here:
What this neat little animation hides though, are some subtle annoyances.
1) The grid sometimes generates triangles, not rhombuses
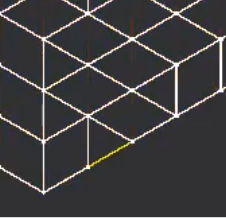
The algorithm works by randomly pairing off triangles into rhombuses. Sometimes that randomisation process will leave an unpaired triangle near the edge. Oskar fixes this by subdividing every shape – the rhombuses become four smaller rhombuses, while the triangles becomes three smaller rhombuses.
This works ok, but it impacts the resolution of the grid. Doubling everything makes the grid look smoother and more regular, as most tiles will be adjacent to at least 3 other tiles that have the identical orientation. Often that is desirable, but I’d rather have the option to not subdivide.
2) The border of each hex is completely fixed
The animation above only shows creating a single hex. To make a larger grid, you repeat the process, and connect all the hexes together. That means the merged rhombuses will never cross the boundary of hexes, so there are some locations where edges are forced to appear.
Oskar applies a relaxation step *after* joining the hexes together (not shown in the above animation), which helps hide this quite effectively, as the hex boundaries are shifted around a little. But it can still be seen with a careful eye. Here’s the townscaper grid with the hexes colored. Note how every border is exactly 8 tiles long.
The Infinite Random Rhombus Grid
So how do I fix these things?
The core of the idea is explained in this video, which describes how to generate random rhombuses to fill a finite sized area.
The idea is that we start with a regular pattern of rhombuses already in place.
Whenever 3 rhombuses meet at a point, it’s possible to rotate them without affecting the rest of the grid.
If you have a finite set of rhombuses, you can shuffle them just by repeating this rotation at random places enough times.
So if we can shuffle finite sections, and we want to generalize to an infinite grid, we can apply the trick I introduce in Infinite Modifying In Blocks. The idea is that we cut the infinite grid up into chunks, and shuffle each chunk separately. But that leaves obvious borders between chunks that are never shuffled. So we repeat the process a second time, using a different chunking arrangement.
After three such shuffles, you’ve left no stone unturned as part of the grid has been shuffled at least once. But there’s still a finite number of chunks that could influence the final arrangement at a given cell, so we can lazily evaluate the right chunks.
An animation will probably explain it better. Each of the three shuffles never crosses the red borders, limiting the range of influence of any random choice. The borders are chosen so every location has a chance of being flipped.
I’ve also made an implementation for Sylves. I’ve shaded the hex chunks here so you can see how the borders are no longer neat.

Random Rectangles
The same swapping trick works for rotating two pairs of rectangles by 90 degrees. This gives a sort of random herringbone look. I’m not sure what other shapes could use the same process.

And again the hexagon is the bestagon – 3 rhombuses make a hexagon