I’ve added an article on handling infinite sized procedural generation to the Sylves documentation. It’s probably of interest to readers of this blog as the techniques are fairly general.
Intermediate
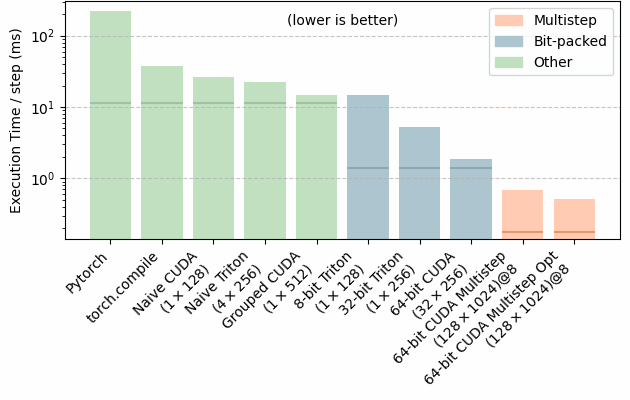
More Accelerated Game of Life
I got a good comment on my previous article about implementing the Game of Life in CUDA pointing out that I was leaving a lot of performance at the table by only considering a single step at once.
Their point was that my implementations were bound by the speed of DRAM. An A40 can send 696 GB/s from DRAM memory to the cores, and my setup required sending at least one bit in each direction per-cell per-step, which worked out at 1.4ms.
But DRAM is the slowest memory on a graphics card. The L1 cache is hosted inside each Streaming Multiprocessor, much closer to where the calculations can occur. It’s tiny, but has an incredible bandwidth – potentialy 67 TB/s. Fully utilizing this is nigh impossible, but even with mediocre utilization we’d do far better than before.
Continue readingAccelerated Game Of Life with CUDA / Triton
Let’s look at implementing Conway’s Game of Life using a graphics card. I want to experiment with different libraries and techniques, to see how to get the best performance. I’m going to start simple, and get increasingly complex as we dive in.
The Game Of Life is a simple cellular automata, so should be really amenable to GPU acceleration. The rules are simple: Each cell in the 2d grid is either alive or dead. At each step, count the alive neighbours of the cell (including diagonals). If the cell is alive, it remains alive if 2 or 3 neighbours are alive. Otherwise it dies. If the cell is dead, it comes ot life if exactly 3 neighbours are alive. These simple rules cause an amazing amount of emergent complexity which has been written about copiously elsewhere.
For simplicity, I’ll only consider N×N grids, and skip calculations on the boundary. I ran everything with an A40, and I’ll benchmark performance at N=216 . For now, we’ll store each cell as 1 byte so this array is which equates to 4 GB of data.
All code is shared in the GitHub repo.
Continue readingClaude is a Ravenclaw
I’m in the midst of doing the MATS program which has kept me super busy, but that didn’t stop me working on resolving the most important question of our time: What Hogwarts House does your chatbot belong to?
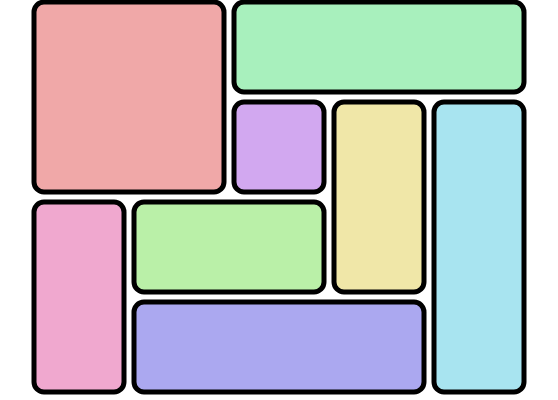
Continue readingExploring Rectangle Subdivisions
Last week, I saw a talk on Vuntra City, a procedurally generated city with a fully explorable city. Developer Larissa Davidova explained that she settled on using Recursive Subdivision for the city blocks, as she wanted some level of organicness, while still only having to deal with rectangles. But she didn’t like having indefinitely long roads that cause implausible sightlines.
One way Vuntra City handles this is by subdividing a rectangle into 5 blocks, a pattern I called “whirl” in my previous article on recursive subdivision. You can see that it has no internal roads that stretch across the entire map.
But Larissa’s talk got me thinking. The whirl pattern is interesting because it cannot be made from simple cuts. What other ways of subdividing a rectangle into smaller rectangles1, are out there?
Continue readingWraparound Hex Grids
A user requested adding wrapping hex grids to Sylves. That is, a grid that is a collection of hexagons, and the collection itself is also hexagonal shaped. When you exit from one side, you re-enter on the opposite side.
The maths for this turned out to be surprisingly fiddly, and not listed by RedBlobGames, so I thought I’d share it here.
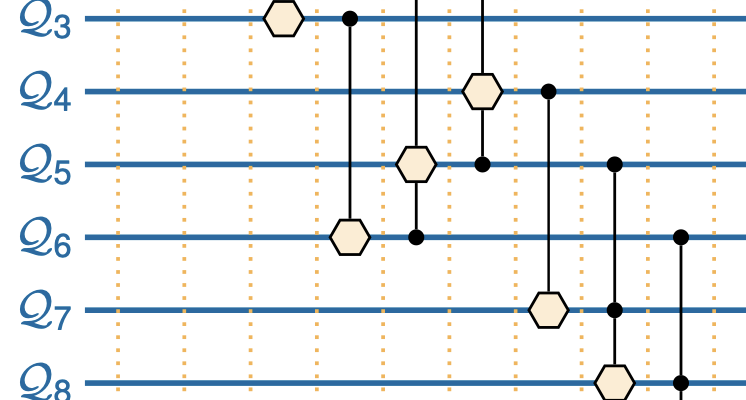
Continue readingQuantum WaveFunctionCollapse
One of my biggest gripes with the WaveFunctionCollapse procedural generation algorithm is that, despite the name, it doesn’t really have anything to do with quantum mechanics. I usually prefer the term Constraint Based Procedural Generation instead.
The name WaveFunctionCollapse is meant more as an analogy. As the algorithm progresses, it resolves a fuzzy, uncertain picture of the output into sharper detail, much as in quantum mechanics, the state of a system is also a range of possibilities, which resolves to something specific when “observed”.
But could we adapt WFC to the Quantum way of thinking, and ran it on actual Quantum Hardware? Well, that’s exactly what is discussed in this new paper Quantum WaveFunctionCollapse by Raoul Heese1 (Youtube summary). Does it work? Is it fast? Let’s find out.
Continue readingInfinite Uniform Point Distributions
Rune’s recent talk on layered procedural generation has got me thinking about procedural generation again, so I wanted to share a technique I found about doing a uniform distribution of points on an infinite plane. I assumed this would be a well known thing, but I couldn’t find any references elsewhere.
Continue readingPublishing An Open-Source Library for Unity
So you’ve got some open source C# code, and you want to publish it for other users in Unity? I’ve explored a few options, here are the pros and cons.
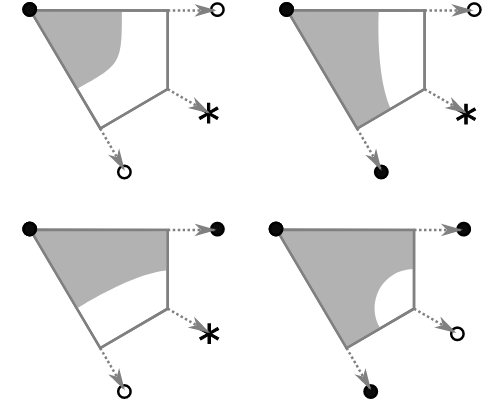
Continue readingOrtho-tiles
Last time, we looked at quarter-tiles. This was an auto-tiling technique for square grids. Each cell in the grid is associated with a terrain (i.e. either solid or empty). Then the squares were split in four, and each quarter was assigned an appropriate quarter-tile.
Otho-tiles extends this procedure to work with irregular grids, even non-square grids. We just have to alter the procedure a little, and be ready to deform the quarter tiles fit in place.
Ortho?
Ortho is a Conway Operator. It can be thought of as the extension of dividing a square into 4. It divides each n-gon into n “kites” or “ortho-cells”. Each kite is a four sided shape containing the cell center, one corner, and the midpoint of the two edges adjacent to that corner.
The appeal of the ortho operation is it can take any polygonal grid, no matter how irregular, and convert it into a grid of 4 sided shapes. And it’s much easier to work with something that has a consistent number of sides.
Continue reading