You are probably familiar with Recursive Subdivision – also known as Binary Space Partitioning – as a procedural generation technique. Like all the best proc gen, it’s a simple idea, that produces complex output. I’m here to discuss some variants that others have used to produce interesting results.

What is Recursive Subdivision

The idea is you start with a large rectangular space, and divide it in two horizontally or vertically. That gives two rectanges, which you can repeat the process to get even smaller, more nested rectangles, and so on.

Note that the terms “recusive subdivision” and “binary space partitioning” mean something different in other CS/gamedev contexts. Use of these things for procedural generation is a tiny fraction of their power.

This technique is classically used for city road networks and mazes.

To make a maze, each subdivision introduces a wall, and then you randomly insert a hole somewhere in that wall. After drawing all the partitions, it’s possible to fully navigate the map, but only by navigating the various holes.

Less commonly, it’s used to generate room-and-passage dungeons reminiscent of Rogue. You apply the subdivisions as normal, but rather than filling each subdivision fully, you put a room in each section, and draw passages between the rooms.

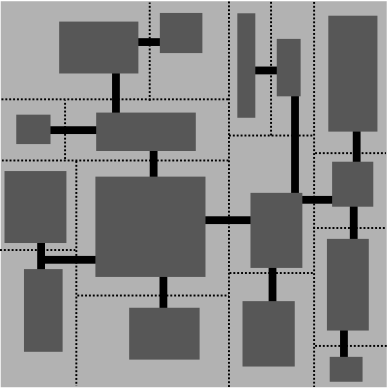
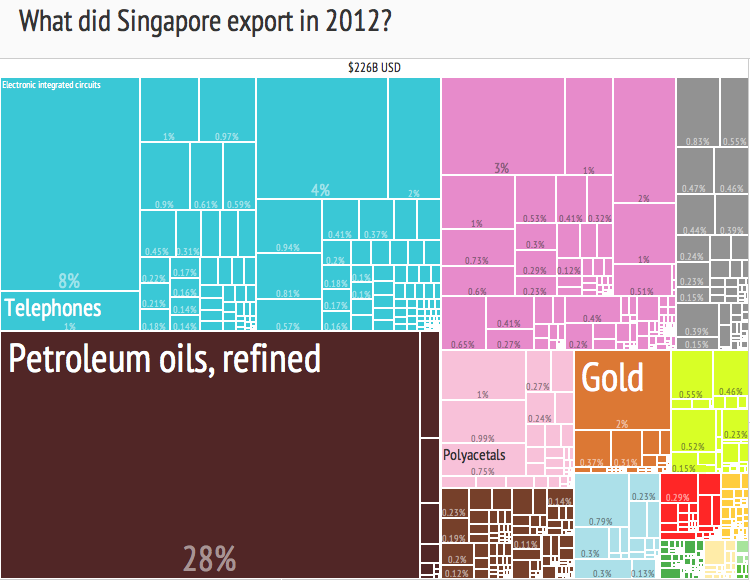
It can also be used to make pretty good charts.

Variants

Basic Bisection

This is the usual case. You have a rectangle, you randomly split it along an axis. Looks basic, but it gives a lot of mileage once you start applying it recursively.

You can customize it somewhat by changing how the split gets chosen. Is it random, or do you always split the longest length. Are splits down the middle, or off to one side?

The main short comings are the fact is only generates rectangles, and the technique is easily revealed as the first subdivision stretch accross the entire area, and usually stands out once you start adding smaller subdivisions.

Polygons

The most obvious addition is to switch from starting with a rectangle, to starting with an arbitrary polygon. Then each slice produces smaller polygons, which we can recurse on. Even better, if you start with a convex polygon the subdivided ones remain convex, which simplifies a lot of difficulty of subdivision.

Bent Subdivision

This kind of polygon partitioning looks promising pic.twitter.com/6QfXoeE3Nt

— Oleg Dolya (@watawatabou) March 19, 2021

If using polygons solves the most obvious “tell” of recursive subdivision, the rectangles, then bent subdivision solves the second, that the earliest slices are really long and stick out. It doesn’t look natural for evolved layouts like roads.

Oleg Dolya proposes solving this by adding exactly one kink to the subdivision. This breaks up the line considerable, and allows both ends of the line to terminate perpendicular to the boundary, and generally adds a level of messiness that I really love.

Oleg has more details on his own page.

Seed Growth

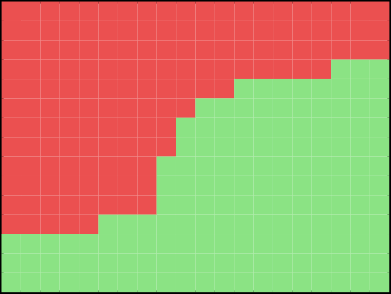
Other way to break up the line is to do some sort of random path instead of keeping things straight. Jamis Buck shows how you can do random cellular growth to get a nicer subdivision. His blog post illustrates the idea very clearly, including animations. Note that as he is using recrusive subdivision to make mazes, the long subvidisions manifest as what he calls “bottlenecks”, choke points that clearly divide the graph in two.

It reminds me a bit of the approach taken by Lenna’s Inception, where different spaces are iteratively grown until they fill the entire area.

Whirl

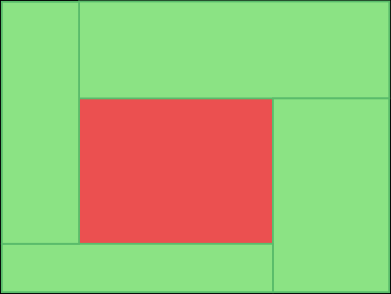
I discovered this subdivision in my Diablo 1 write up where it is used in the catacombs levels. It divides the level into 5 sections – one central one and 4 surrounding pieces. I really like it as it’s dead simple, but it avoids having too long a cut. The asymmetry of the central square vs the outer ones also leads to a lot more interesting patterns – realistically, most cities / dungeons / whatever are not uniformly dense, and often have more going on in center than the edges.

Grid

I’m sure this technique is used all over the place, but it’s used to great effect in this write-up of Pokemon Mystery Dungeon’s level generation. This is the only subdivision scheme that looks more regular than the basic subdivision, so it definitely has its uses.

Pokemon Mystery Dungeon in particular gets more milage out of using a grid by sometimes treating certain cells differently:

• Keep a cell entirely empty
• Keep a cell empty, except for passageways travelling to other cells
• Randomly merging adjacent cells

NB: The equivalent for polygonal systems would be Voronoi partitioning, I guess.

OffGrid

This page documents a rectangle based scheme that looks irregular, but it very easy to compute.

Non-Division

If you are recursively dividing, there’s no obligation to divide to the same depth everywhere. This can be used to keep some large spaces available, or add some non-uniformity.

---

That’s it. Let me know if you’ve seen some other neat techniques in this area.