Beginner

This category contains articles suitable for most readers just starting out.

See Intermediate and Advanced for more articles.

Dihedral Subgroups Explained Via Factorio

| Boris

The dihedral group is the mathematical formalism behind all the rotations and reflections of a regular polygon. For an n sided polygon, there are always n possible rotations, and n reflections, for 2n possible symmetries.

Combining any two symmetries gives another from the same group, that is what makes it a group in the mathematical sense.

The theory of it is useful to know for gamedev. I was reminded of this when seeing this Factorio devlog, where the developer ran into some trouble because he initially forgot to account for all the cases.

Continue reading →

Next Token Prediction is a Misleading Term

| Boris

I’m fed up of hearing about how LLMs are next token predictors, and therefore they <cannot do some task> <aren’t really doing cognition> <are just guessing>.

There’s lots of philosophical objections, but fundamentally, framing AI as next token predictors in the first places is just misleading and inaccurate. Here’s why LLMs aren’t naive next token predictors.

Continue reading →

Fiddling Weights with Temperature

| Boris

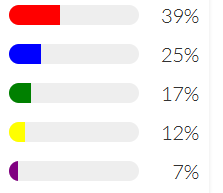
In procedural generation, the absolute simplest, most common technique is randomly picking an item from a list. More often than not, it is a weighted random choice, where each item is selected with a frequency proportional to its “weight”, a numerical value that can be tweaked by the designer.

def random_choice(items: list, weights: list[float]):
    total_weight = sum(weights)
    random_value = random.random() * total_weight
    
    # Find the item that corresponds to the random number
    for i, weight in enumerate(weights):
        random_value -= weight
        if random_value <= 0:
            return items[i]

I wanted to share a technique from the Machine Learning community that is simple enhancement to this routine that gives a lot of convenience over tweaking weights directly, called temperature.

Continue reading →

What Is Procedural Generation

| Boris

Procedural Generation can be interpreted quite broadly as just “making computers make cool creative things”. People make art, games, music, audio, stories and all sorts of weird things.

I’ve been doing it as a hobbyist for some time, and have become more and more involved: I make tutorials, projects, I sell a tool online for a niche algorithm, and recently taught a “masterclass” at Everything Procedural, the main conference for professionals in the space.

I thought I’d spill some digital ink about what it’s actually about. I get asked often enough, and this will help me clarify my verbal answers.

Continue reading →

0.999… = 1, with Rigour

| Boris

I’ve recently seen a lot of demonstrations of why the decimal 0.999… equals 1.

These are endlessly cycling the internet, simply because all the simple explanations aren’t really compelling. You see smart people responding “can’t you just…” or simply not convinced by bare assertion.

The truth is that is that dealing with these things is actually a lot more complex than a glib twitter answer. You should feel uneasy with these explanations. This same subject confused mathematicians of earlier centuries, leading to awkward theories like “infinitesimals”, which ultimately fell out of favour.

I’m going to take you through a proof that 0.999… = 1, with rigour. Rigour is a term used in maths for building from a solid foundation and proceeding from there in sufficiently small steps. Thus, the majority of the article is not the proof but the definitions. How can we talk about infinity in a way that makes sense? The trick, as we’ll see, is to only talk about finite things we already understand, and define infinity in terms of those.

This article is aimed at those with high school level maths. There’s a proof halfway down, but it’s skippable.

Continue reading →

Model Synthesis and Modifying in Blocks

| Boris

I’ve written a lot about Wave Function Collapse. Developed in 2016 by Maxim Gumin, it’s an algorithm for generating tilemaps and pixel textures based on the constraint solving with extra randomization . But did you know most of the key ideas come from a paper written a full decade earlier? Today, we’ll be looking into Model Synthesis, the 2007 PhD dissertation of Paul Merrell, and some of the elaborations he’s designed, particularly Modifying in Blocks.

Continue reading →

Arc Consistency Explained

| Boris

I’ve been doing a lot of experiments with WaveFunctionCollapse, which as we’ve covered before, is essentially a constraint solver turned into a procedural generator.

The underlying solver WaveFunctionCollapse came with is called Arc Consistency 3, or AC-3 for short. But AC-3 is actually one of a whole family of Arc Consistency algorithms. Today, my solver and most others uses AC-4, a more advanced algorithm. Let’s talk a bit about how those both work.

Continue reading →

Recursive Subdivision Variants

| Boris

You are probably familiar with Recursive Subdivision – also known as Binary Space Partitioning – as a procedural generation technique. Like all the best proc gen, it’s a simple idea, that produces complex output. I’m here to discuss some variants that others have used to produce interesting results.

Continue reading →