It’s been over a year since I last deconstructed how a game does its procedural generation. Today we’ll be looking at Planet, a 2016 cosy design toy by one of my favourite developers, Oskar Stålberg.
Continue readingHow does Planet Work
gamedev
Everything you need to know about Quaternions for Game Development
Defining Chess Piece Moves using Regular Expressions
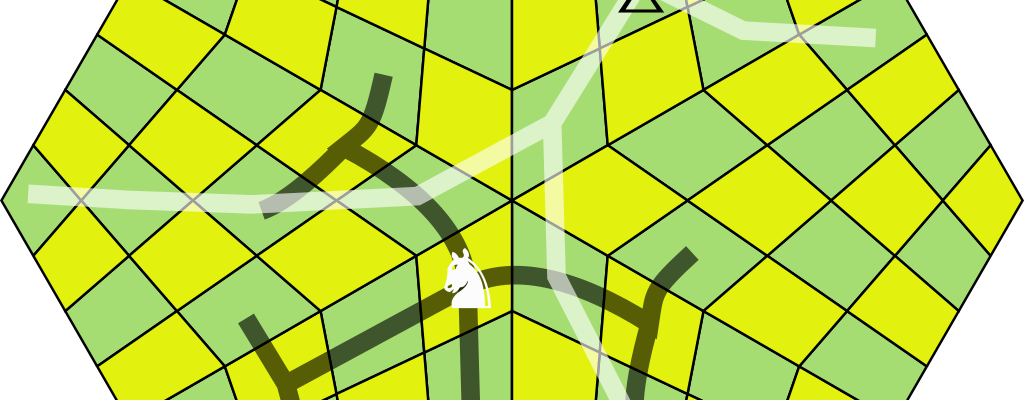
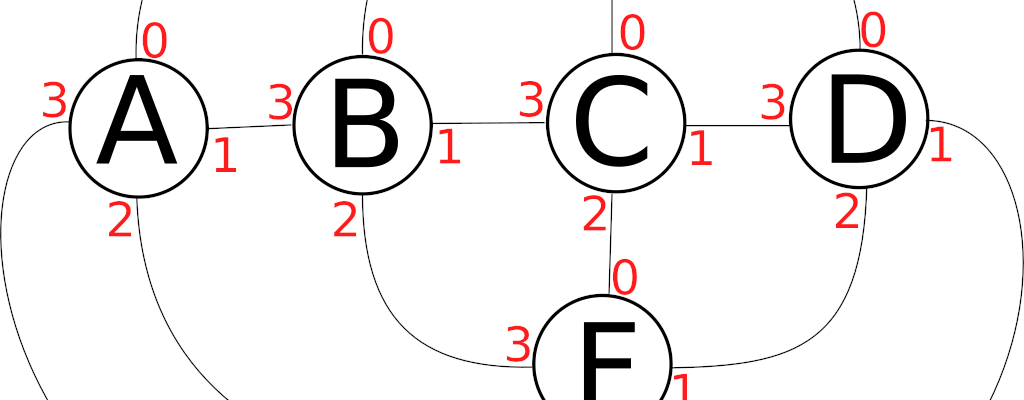
Suppose you wanted to code a simple chess game. One key bit of game logic is to describe what are legal moves for each piece. There’s only 6 types of piece (pawn, knight, bishop, rook, queen, king) so this isn’t exactly a hard task. You can write rules such as:
def canRookMove(from, to):
# Ignores questions about colliding with other pieces
return (from.x == to.x or from.y == to.y) and from is not toBut these days, I’ve been thinking a lot about grids, and the above approach just doesn’t generalize. What if you wanted to play chess on a stranger grid?
What would it mean to play chess on the grid above, or a hexagonal grid, and so on? You’d have to write a whole new set of rules, and they could get very complicated depending on the grid in question. What I want is a language that describes how pieces move, which generalizes to any board. And I think I’ve found it, using regular expressions.
Continue readingVoronatorSharp
I’ve relased a new library, VoronatorSharp.
VoronatorSharp is a C# library that computes Voronoi diagrams. The Voronoi diagram for a collection of points is the polygons that enclose the areas nearest each of those sites.
Voronoi diagrams have applications in a number of areas such as computer graphics.
This library features:
- Computes Voronoi diagrams and Delaunay triangulations.
- Voronoi polygons can be clipped to a rectangular area.
- Uses a
n log(n)sweephull algorithm. - The implementation attempts to minimize memory allocations.
- Integrates with Unity or can be be used standalone.
- Uses robust orientation code.
- Handles Voronoi diagrams with only 1 or 2 points, and collinear points.
Rotation Graphs
Graphs are a data structure we’ve already talked a lot. Today we’re looking at extension of them which is both obvious and common, but I think is rarely actually discussed. Normal graphs are just a collection of nodes and edges, and contain no spatial information. We’re going to introduce rotation graphs (aka rotation maps) that contain just enough information to allow a concept of turning left or right – i.e. rotation.
Continue readingMosaic Paint
As a side-project of a side-project, I’ve made a little painting program. It’s like a normal paint program, only you paint on a tile grid instead of pixels. You can create mosaic and stained-glass style images.
Continue readingEditable WFC
When I spoke about autotiling, I briefly touched on how it’s possible to use Wave Function Collapse (or other constraint based generators) as a form of autotiling, i.e. user-directed editing of tilemaps.
I’ve usually referred to this technique as “editable WFC“. It’s a combination of autotiling and WFC, and contains the best of both:
- Being an autotiler, it allows users to easily and interactively make changes to an existing level.
- Being constraint based, it automatically ensures that those changes are consistent with the predefined rules of the constraints, potentially making further changes to the level to make it fit
This is different from most other autotilers, which either require manual configuration of patterns used to enforce good behaviour, hidden layers, or come with more stringent requirements on what tiles are available.
Continue readingChiseled Paths Revisited
Back in 2017, I described a method of random path generation called Chiseling. It gives very nice wiggly paths, but I was never satisifed with the performance. I later revisited it, and found a faster algorithm, but it was a bit complicated to implement.
I’m pleased to say that I think I’ve finally found a way of implementing it that is both fast and simple.
Continue readingResolving Ambiguities in Marching Squares
One issue with 2d Marching Cubes (i.e. Marching Squres) that I glossed over in my original tutorial is the issue of ambiguity. Later I talk about how dual contouring avoids this problem. But it turns out there’s actually a well known, but little documented way of resolving those ambiguities called the Asymptotic Decider, which I’ll explain below.
Continue reading2d Marching Cubes with Multiple Colors
2d Marching cubes (sometimes called marching squares) is a way of drawing a contour around an area. Alternatively, you can think of it as a drawing a dividing line between two different areas. The areas are determined by a boolean or signed number value on each vertex of a grid:
But what if we didn’t have a boolean value? What if we had n possible colors for each vertex, and we wanted to draw separating lines between all of them?
Continue reading